How AI Video Generation Works: A Deep Dive into Diffusion Models for Video
Date: Jan 27, 2026
There's been an explosion of development in AI video generation. Recent models like Wan2.1 and Wan2.2 from Alibaba can now generate remarkably coherent videos from text prompts. But how do they actually work? What's different compared to image generation?
It turns out that modern video generation models are very similar to stable diffusion: we train a VAE to encode videos into a latent space, and then we train a diffusion model to sample from this latent space (conditioned on a text description of the video). The main difference when compared to previous models like Stable Diffusion, is that the VAE produces a voxel latent tensor and the diffusion model is a transformer model.
To explore modern video generation models I created a basic example using videos of translating MNIST digits. This post will walk through the basic components of video generation models and how to train them.
Generative Modeling: Sampling from an Unknown Distribution
At its core, generative AI solves a simple problem: given examples from some distribution, generate new examples from that same distribution.
The problem? We don't have p(data). We can't write down an equation for
"the distribution of all realistic photographs." What we do have is a finite
collection of samples: our training dataset.
This is the fundamental challenge of generative modeling. Different approaches tackle it differently:
- GANs train a generator to fool a discriminator that tries to distinguish real from fake samples
- VAEs learn a latent space where sampling is easy, then decode to data space
- Autoregressive models factor the distribution as a product of conditionals: p(x) = p(x₁)p(x₂|x₁)p(x₃|x₁,x₂)...
- Diffusion models learn to reverse a gradual noising process
Learning to Transform Distributions
Here's the key insight that unifies all these approaches: we know how to sample from simple distributions.
Furthermore, probability theory tells us that given a suitable function, we can map one random variable into another distribution. If we have this transformation function and we can sample from the first random variable, then we can sample from second random variable.
So the strategy becomes: learn a transformation that maps samples from a simple distribution to samples from the data distribution.
z ~ N(0, I) # Easy to sample
x = T(z) # Learned transformation
x ~ p(data) # What we want
Different generative models learn this transformation T in different
ways:
- GANs learn
Tdirectly as a neural network (the generator), trained adversarially - VAEs learn
Tas a decoder, with an encoder that maps data back to the simple distribution - Normalizing Flows learn
Tas a sequence of invertible transformations with tractable Jacobians - Diffusion models take a different approach—they learn the gradient of a transformation, then integrate it
The Score Function Perspective
So how do we transform from one distribution into another? Diffusion models iteratively refine samples from the simple distribution to increase their likelihood in the data distribution. To understand this consider the score function defined as:
∇ₓ log p(x)
This gradient points toward regions of higher probability. If you're at a noisy image, the score tells you which direction leads toward realistic images. You don't need to know the actual probability values, just the direction of improvement.
Diffusion models learn an approximation of this score function at various noise levels. When we denoise, we're essentially following the score—taking steps toward the high-probability region where real data lives.
This is why the training objective works: by learning to predict and remove noise, the model implicitly learns the structure of the data distribution. Each denoising step moves the sample closer to the data manifold.
What Are Diffusion Models?
If we take a real image and progressively add noise to the image, eventually it mostly resembles a Gaussian image, something we can sample from. If we keep track of the added noise, we can teach a neural network to "reverse" this noise process and recover the original image.
Effectively the reverse process is the transformation that turns a Gaussian image into a real image.
Adding noise is typically referred to as the forward process and reversing the noise is referred to as the reverse process.
- Forward process: Gradually add noise to real data until it becomes pure random noise (which we can sample from!)
- Reverse process: Train a neural network to reverse this—to remove noise step by step
Mathematically, the forward process is defined as:
x_t = √(1-beta_t) * x_{t-1} + √(beta_t) * ε
Where x_t is the corrupted sample at timestep t obtained
after applying t steps of corruption to original data, ε
is random Gaussian noise, and beta_t is a scheduled value that controls
the noise level at timestep t. At t=0, you have clean
data. At t=T (say, 1000), you have nearly pure noise.
The model learns to predict the noise ε that was added, given the noisy
sample x_t and timestep t. During generation, we start
from random noise and iteratively subtract the predicted noise.
From Diffusion to Stable Diffusion: Why Use a VAE?
Early diffusion models operated directly in pixel space. For a 512×512 RGB image, that's 786,432 dimensions the model must handle at every denoising step. This works, but it's computationally expensive.
Stable Diffusion introduced a key insight: we don't need to denoise in pixel space. Instead:
- Train a Variational Autoencoder (VAE) to compress images into a compact latent space
- Train the diffusion model to generate in this latent space
- Decode the generated latents back to pixels
The VAE typically compresses images by 8× in each spatial dimension. A 512×512 image becomes a 64×64 latent with 4 channels—that's only 16,384 dimensions, a 48× reduction. The diffusion model can now focus on semantic structure rather than pixel-level details, while the VAE handles the translation to and from high-resolution pixels.
This isn't just about speed. Operating in latent space provides an information bottleneck that forces the model to learn meaningful representations. The VAE captures local texture and detail; the diffusion model captures global structure and semantics.
A VAE on its own could be used to learn a generative model of the training data, but in this case we use it more as a regularized autoencoder.
Text Conditioning in Real Models
So how do we teach the diffusion model to sample VAE latent vectors based on the input text? It turns out, when using a transformer model for the diffusion model, handling the text is pretty simple. We can embed the text into token space and then use cross-attention with the other input tokens.
Text Encoding
First, the text prompt is converted into a rich embedding using a pretrained language model:
# Conceptually:
text = "A cat walking through a garden"
text_tokens = tokenizer(text) # Convert to token IDs
text_embeddings = text_encoder(text_tokens) # [seq_len, embed_dim]
The key insight is that the chosen text encoders are pretrained and frozen—the diffusion model learns to work with whatever representations they produce.
Cross-Attention
The text embeddings are incorporated via cross-attention layers in the transformer. That is we use a transformer layer, the noise tokens are used for the query and the text embeddings are used for the keys and the values. We then add the output of this layer to the original input and this effectively "conditions" the noise tokens.
This way each video token can attend to all text tokens, allowing the model to incorporate semantic information from the prompt at every spatial and temporal location.
Classifier-Free Guidance
One of the most important techniques in conditional generation is classifier-free guidance (CFG). It dramatically improves sample quality and prompt adherence.
The Problem
A model trained with conditioning can generate samples that match the prompt, but they might be generic or low-quality. We want samples that are strongly aligned with the prompt.
Training with Dropout
During training, we randomly drop the conditioning with some probability (typically 10-20%):
This trains the model to generate both conditionally and unconditionally. When conditioning is dropped, it learns the general distribution of videos. When conditioning is present, it learns the conditional distribution.
Guided Sampling
To apply guidance, remember that the diffusion model at every timestep is predicting the direction to "move" the current sample. When we use text conditioning we change the "direction" to point towards a higher likelihood direction relative to the text prompt.
Without the text input, we get an unconditional direction that is purely based on the data likelihood. We can blend between these two directions to control the guidance amount.
We run the model twice—once with the prompt, once without—and extrapolate.
The guidance scale controls how strongly we push toward the conditional prediction:
- guidance_scale = 1.0: No guidance, just use the conditional prediction
- guidance_scale = 7.5: Typical value, strong prompt adherence
- guidance_scale > 10: Very strong adherence, but can cause artifacts and oversaturation
Mathematically, we're computing:
ε_guided = ε_uncond + s * (ε_cond - ε_uncond)
= (1 - s) * ε_uncond + s * ε_cond
When s > 1, we're actually extrapolating beyond the conditional
prediction, pushing the sample further in the direction indicated by the prompt.
Why Does This Work?
The intuition: (ε_cond - ε_uncond) represents the "direction" that the
conditioning adds. By scaling this up, we amplify the effect of the prompt. The
model generates samples that are more stereotypically aligned with the text
description.
The downside is that high guidance scales reduce diversity—all samples of "a cat" start looking similar—and can introduce artifacts. Finding the right guidance scale is a tradeoff between quality, diversity, and prompt fidelity.
Negative Prompts
A popular extension is negative prompts. Instead of using a null embedding for the unconditional path, we use an embedding of things we want to avoid:
def guided_sample_with_negative(model, x_t, t, pos_embed, neg_embed, guidance_scale):
eps_neg = model(x_t, t, neg_embed) # "blurry, low quality"
eps_pos = model(x_t, t, pos_embed) # "a beautiful sunset"
eps_guided = eps_neg + guidance_scale * (eps_pos - eps_neg)
return eps_guided
This pushes the sample away from the negative prompt while pulling toward the positive prompt.
A Minimal Video Dataset: Moving MNIST
To demonstrate video generation without requiring massive compute, we created a simple synthetic dataset: Moving MNIST. Each video shows a single MNIST digit moving upward across frames.
Despite its simplicity, Moving MNIST captures the essential challenge of video
generation: temporal coherence. The model must understand that frame
t+1 should show the digit slightly higher than frame t,
maintaining consistent appearance throughout.
Here are some examples:
digit 3
digit 9
Video as a 4D Tensor
The fundamental difference between image and video generation is dimensionality. An
image is a 3D tensor: C × H × W (channels, height, width). A video adds
the time dimension: T × C × H × W.
This extra dimension has profound implications for the entire architecture. Every layer that processes the data must now reason about temporal coherence—ensuring that frame 5 looks like a natural continuation of frame 4.
The Two-Stage Architecture
State-of-the-art video generation models like Wan2.1 and Wan2.2 use a two-stage architecture:
- 3D VAE (Variational Autoencoder): Compresses videos into a compact latent space
- Diffusion Transformer: Learns to generate in that latent space
This is the same pattern used by Stable Diffusion for images, but adapted for video. Let's examine each component.
Stage 1: The 3D Convolutional VAE
Why 3D Convolutions?
For images, we use 2D convolutions that slide a kernel across height and width. For video, we need 3D convolutions that slide across time, height, and width simultaneously. This allows the network to learn spatiotemporal features—patterns that exist across both space and time.
Asymmetric Downsampling
A key design choice: we downsample spatial dimensions more aggressively than temporal ones.
If we start with a video of shape [T=16, H=32, W=32], the latent becomes
[T=8, H=8, W=8]. We preserve more of the temporal resolution because
temporal coherence is critical for video quality. Models like Wan2.1 follow similar
principles—compressing spatially while being more conservative temporally.
Modern models leave the latent space produced by the encoder as a 4 dimensional tensor, typically referred to as a voxel latent space. The decoder can then take the generated or sampled latents and upsample them back to the original video size.
Stage 2: The Diffusion Transformer
Once we have a trained VAE, we freeze it and train a diffusion model to generate in the latent space. Modern video models like Wan2.1 and Wan2.2 use transformers rather than U-Nets for this stage.
Flattening Video to Sequences
Transformers operate on sequences. We flatten our 3D latent into a 1D sequence of tokens:
For a latent of shape [4, 8, 8, 8], this gives us
8 × 8 × 8 = 512 tokens. Each token represents a small spatiotemporal
patch of the video.
Positional Encodings
Without positional information, the transformer can't distinguish frame 1 from frame 10, or the top-left from bottom-right. We add sinusoidal positional embeddings:
More sophisticated models use separate temporal and spatial encodings, or learned 3D positional embeddings. Wan2.1 uses RoPE (Rotary Position Embeddings) for better length generalization.
Conditioning
We can condition generation on various signals. In this example, we condition on digit class, so our text conditioning is just a 1-hot encoded vector representing the digit.
Real models like Wan2.1 condition on text embeddings from language models, using cross-attention mechanisms to incorporate rich semantic information.
Additionally the diffusion model needs to know what noise level it's denoising from. So we also embed the timestep and add it to all tokens.
Noise Scheduling: DDPM vs Flow Matching
There are two popular frameworks for training diffusion models.
DDPM (Denoising Diffusion Probabilistic Models)
The classic approach. We define a forward process that gradually adds noise.
x_t = √(1-beta_t) * x_{t-1} + √(beta_t) * ε
The model is then trained to reverse this process by prediction the noise
ε at each timestep t so that we can subtract it out.
As written, to create the training target for timestep t we would have
to run the noise process from the beginning up to time t which is
inefficient. A key realization is that we can derive a one step formula for the
noise at time time t in terms of the original data sample
x_0:
x_t = √(\bar{alpha}_t) * x_0 + √(1-\bar{alpha}_t) * ε
where
\alpha_t = 1-\beta_t
\bar{alpha_t} = \cumprod_{i=1}^t \alpha_i
The input to the model is then x_t and the training target is just the
noise ε. The model learns to predict the noise based on the calculated
x_t, and we reverse the process step by step during sampling.
Flow Matching
A newer approach that's gaining popularity. Here the corruption process is a linear
interpolation between the original data sample x_0 and the noise.
x_t = (1-t)x_0 + tε
The model is then trained to predict the rate of change or 'velocity' of this equation and we can reverse it by integrating the velocity
dxt/dt = ε - x_0
While this may look like a constant, it is important to remember that the noise is a
random variable and thus so are the x_t and velocity. The model learns
to predict an expected value of the velocity at any given time step
v_θ(x_t, t) ≈ E[ε - x₀ | x_t, t]
Flow matching often trains faster and produces better samples with fewer steps. Many recent models, including variants of Wan, use flow matching or similar rectified flow approaches.
Putting It All Together
So the full training and sampling process for our video generation model is
- Train a 3D convolutional VAE on the MNIST videos
- Encode every video into its latent voxel representation
- Train a diffusion transformer, conditioned on the digit class, to sample the
latent voxels
- use either DDPM or flow matching for the training objectives and sampling
- Take samples from the diffusion model and decode them into videos using the VAE decoder
Here are some of the final samples from our model:
digit 9
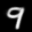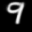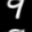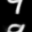
digit 6
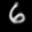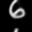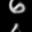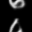
Conclusion
Video generation extends image diffusion in conceptually straightforward ways:
- Add the time dimension everywhere
- Use 3D convolutions in the VAE
- Flatten spatiotemporal tokens for the transformer
- Everything else (noise schedules, training objectives, sampling) stays remarkably similar
The challenges are in the details: balancing the VAE's KL divergence for good latent spaces, designing attention patterns that capture long-range temporal dependencies, and scaling to the massive compute required for high-resolution, long-duration video.
Understanding these fundamentals gives you the foundation to explore state-of-the-art models and perhaps contribute to the next breakthrough in AI video generation.
The code examples in this post form a minimal but complete video diffusion system. You can find the full implementation in the accompanying repository.